En este segundo post presentamos los resultados de comparar la búsqueda dicotómica (que es el mejor algoritmo de búsqueda que hay hasta ahora) con el nuevo algoritmo presentado.
Hipótesis inicial
Antes de continuar tendrías que leer el primer artículo de esta serie.
Partimos de que en la búsqueda dicotómica el número de veces que se ejecuta el algoritmo es de log(N), siendo N la longitud del vector. Por otra parte en el algoritmo propuesto, el número de veces que se tiene que ejecutar es constante en teoría. No depende de la longitud del vector, ya que en cada ejecución no busca la mitad del vector sino que busca un candidato a ser la posición que se desea encontrar.
Es por ello que la hipótesis es que cuanto más largo es el vector, más rápido es el algoritmo propuesto respecto al algoritmo de búsqueda dicotómica.
Por otro lado, como este algoritmo tiene una carga de cálculo mayor que el algoritmo de la búsqueda dicotómica, es posible que cuanto mayor sean los números que hay en el vector, más lento irá el algoritmo propuesto, respecto al algoritmo de la búsqueda dicotómica.
Material y métodos
Como el tiempo en que se tarda en buscar un elemento en un vector, tanto en un algoritmo como en el otro es casi 0, se procedió de la siguiente manera:
Para confirmar la primera hipótesis, se creó un bucle donde en cada iteración se crearon 1000 vectores de forma aleatoria, todos con el mismo tamaño entre ellos y un valor máximo para cada elemento de los vectores. Para cada uno de estos vectores, se ordenan y se mide el tiempo en que se busca en los 1000 vectores un elemento aleatorio, tanto en el algoritmo propuesto como en la busqueda dicotimica. Una vez hecho esto se incrementa el tamaño del vector, para que en la siguiente iteración los algoritmos de búsqueda se ejecuten sobre un vector más grande, que el anterior. Todos estos resultados se guardan en una base de datos. Así tenemos como se comporta cada algoritmo según se aumenta el tamaño de los vectores.
Finalmente en la base de datos, tenemos para cada iteración hecha, el tiempo que se ha tardado en ordenar los 1000 vectores en los dos algoritmos y el número de posiciones que tenían los vectores.
Para confirmar la segunda hipótesis se procedió de forma similar. Lo única diferencia es que en vez de variar el tamaño del vector, lo que varia en cada iteración es el valor máximo, permitiendo que en cada ejecución, los valores del vector sean mayores.
Resultados
En lo que respecta a la hipótesis primera (el algoritmo irá mejor cuanto mayor sea la longitud del array) Estos son los resultados:
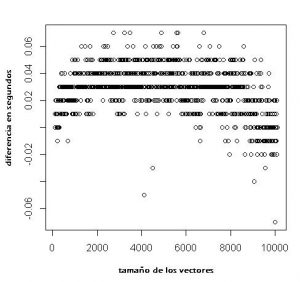
Figura 1. Gráfico que muestra la relación de la diferencia de tiempo entre los dos algoritmos con el tamaño de los vectores, empezando por un tamaño de 100 posiciones y añadiendo 10 posiciones en cada iteración del bucle hasta vectores de tamaño 10000.
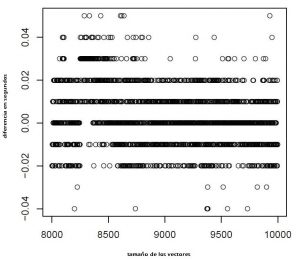
Figura 2. Gráfico que muestra la relación de la diferencia de tiempo entre los dos algoritmos con el tamaño de los vectores, empezando por un tamaño de 8000 posiciones y añadiendo 10 posiciones en cada iteración del bucle hasta vectores de tamaño 10000.
En la figura 1 y 2 se ve como en casi todos los vectores con tamaño menor o igual a 8000 posiciones se busca más rápido con el algoritmo propuesto. Mientras que a partir de 8000 el rango de diferencias entre los dos algoritmos es más amplio. De todas formas se ve como de 100 a 8000 posiciones hay algunos bucles donde la búsqueda dicotómica es más rápida que el algoritmo propuesto. También se puede divisar que entre 100 a 6000 posiciones la diferencia entre ambos algoritmos es más grande, de 6000 a 8000 la diferencia se acorta aunque aún es mejor el algoritmo propuesto y es a partir de 8000 cuando la busqueda dicotomica empieza a tener menores tiempos de cálculo.
En lo que respecta a la segunda hipótesis – cuantos mayores son los números que contiene el vector más tarda el algoritmo propuesto – estos son los resultados:
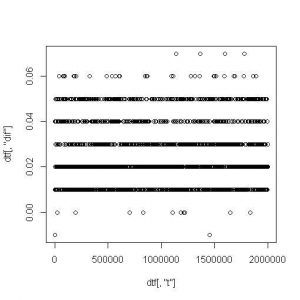
Figura 3. Grafico que muestra la relación de la diferencia de tiempo entre los dos algoritmos con el número máximo que contiene el vector, empezando por un máximo de 1000 y aumentando 1000 el número máximo hasta llegar a un número máximo de 2000000.
Aquí se demuestra que nuestra segunda hipótesis es incorrecta ya que la diferencia entre los tiempos de los dos algoritmos no se ve alterada con el aumento del valor de los números que contiene el vector.
Discusión
Aunque el número de iteraciones que hace el algoritmo propuesto es constante, también es cierto que la longitud del vector se tiene en cuenta a la hora de adivinar la posición del valor buscado. Es por ello que cuanto mayor sea la longitud del vector mayor, más complejo será el cálculo para adivinar la posición y más tiempo llevará realizarlo.
Es por ello, desde 0 a una cierta longitud, el algoritmo propuesto es más rapido ya que acierta mejor a la hora de elegir el candidato mientras que a partir de una cierta longitud de vector aunque ese acierto sigue estando es contrarestado con el tiempo que se tarda en elegir el candidato.
Por otro lado, el algoritmo propuesto solo funciona correctamente si los elementos del vector tienen una distribución geométrica o parecida a ella. Cuando la distribución de los elementos del vector tiene una distribución exponencial o parecida a ella, el tiempo de búsqueda para este algoritmo es proporcional a N (siendo N la longitud del vector) Por esta razón incluso en vectores de tamaño menor o igual que 8000, el tiempo de búsqueda por algoritmo propuesto es mayor que el algoritmo de búsqueda dicotómica.
Conclusiones
En término medio, en vector de tamaño igual o menor de 8000 elementos el algoritmo propuesto es mejor el algoritmo de búsqueda dicotómica.